Chapitre CTM5 – Réactions d’oxydo-réduction (exercices)
Exercices possibles sur les piles, sur les titrages directs et indirects.
Chapitre OS7 – Filtrage linéaire
Questions de cours :
- Définir la valeur moyenne et la valeur efficace, et l’appliquer à un signal sinusoïdal quelconque.
- Définir ce qu’est un spectre en amplitude pour un signal périodique, donner la décomposition en série de Fourier en définissant chaque terme. Sur un exemple de décomposition de signal au choix du colleur, représenter le spectre en amplitude.
- Étudier complètement le filtre passe-haut d’ordre 1 (circuit RL) : fonction de transfert (forme canonique), comportement asymptotique, gain et déphasage, diagramme de Bode asymptotique en gain et phase.
- Définir rigoureusement la pulsation de coupure et la calculer pour un filtre passe-bas et passe-haut du premier ordre (à partir de fonctions de transferts fournies).
- À partir d’un signal
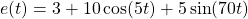, expliquer qualitativement comment obtenir le signal en sortie d’un filtre passe-bas (
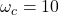) ou passe-haut (
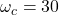). - Présenter quelques fonctions : moyenneur, intégrateur, dérivateur et des exemples de circuits en précisant les conditions pour lesquelles ils jouent correctement leur rôle.
- Donner la définition de la fonction de transfert, de l’impédance d’entrée et de sortie, et déterminer la condition pour associer deux quadripôles de sorte que la fonction de transfert globale soit le produit des fonctions de transfert individuelles.
Exercices sur des filtres d’ordre 1 ou 2, exploitant des graphiques, calculant des fonctions de transfert, des asymptotes, des gabarits,…
Chapitre OS8 – Ondes et interférences (cours uniquement)
Questions de cours :
- Donner sans démonstration les deux formes mathématiques par lesquelles on peut modéliser une onde progressive quelconque se propageant à la célérité
dans le sens des 
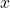croissants. Que deviennent ces deux formes dans le cas où l’onde se propage dans le sens des 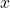décroissants ? - Présenter l’onde progressive sinusoïdale, avec la formule selon le sens de propagation, la double périodicité. Démontrer la relation liant la longueur d’onde, la période et la célérité d’une onde progressive sinusoïdale.
- Présenter le phénomène d’interférences. Montrer, dans le cas de signaux sinusoïdaux synchrones et en phase issus de points
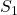et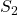 
que la connaissance de la différence de marche 
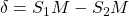en un point 
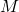de l’espace permet de connaître si les interférences sont constructives ou destructives. - Présenter l’expérience des fentes d’Young et calculer la différence de marche dans l’approximation paraxiale.
- Donner la formule de Fresnel, l’appliquer au cas des fentes d’Young où
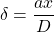. Interpréter qualitativement, puis déterminer l’interfrange.